Computational Category Theory in Applied Mathematics

Owen Lynch and James Fairbanks

Overview

1. Why is AlgebraicJulia?
2. Who is AlgebraicJulia?
3. What is AlgebraicJulia?
4. How is AlgebraicJulia?
5. Why again is AlgebraicJulia?

Part 1: Why is AlgebraicJulia?

Compositional modeling

Halter et al. (2020)

• One of the rallying cries of applied category theory is “compositionality”.
• The AlgebraicJulia project takes compositionality and makes it work in software tools for scientists

But why is this a good idea; why do we expect that scientists will want to use compositional tools?

“Informal diagrams that should be String Diagrams”

Figure 1: Informal diagrams in the wild

• We see diagrams that look like this all the time in the wild
• This proves that scientists want to think in highlevel formalizations
• But when it comes time to make their models run on the computer, they have to use low-level formalizations, like general-purpose programming languages
• “The model is the code”

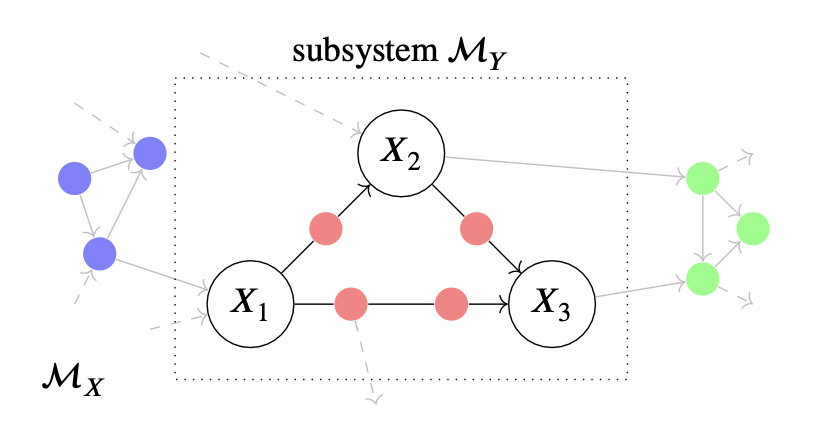
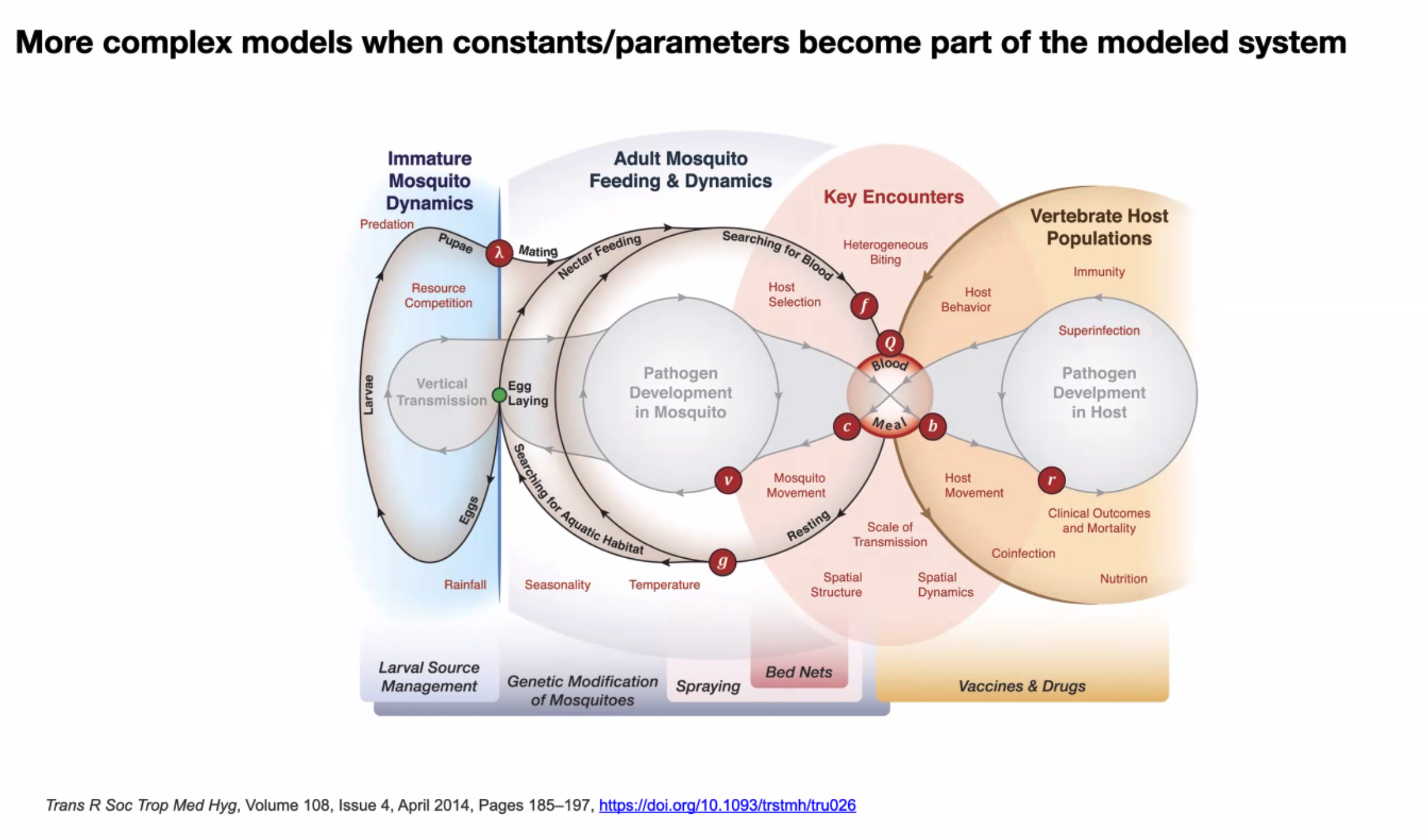
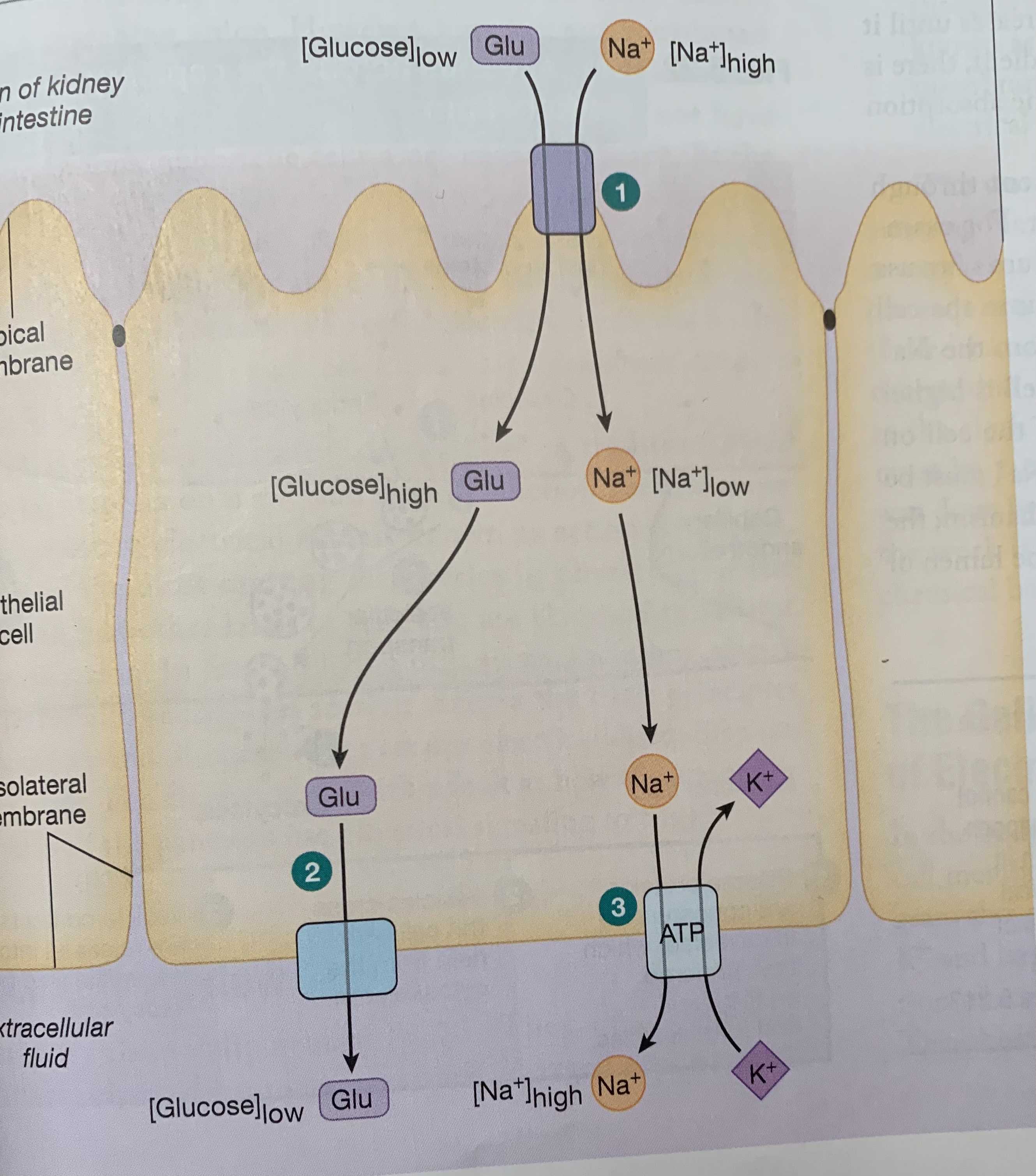
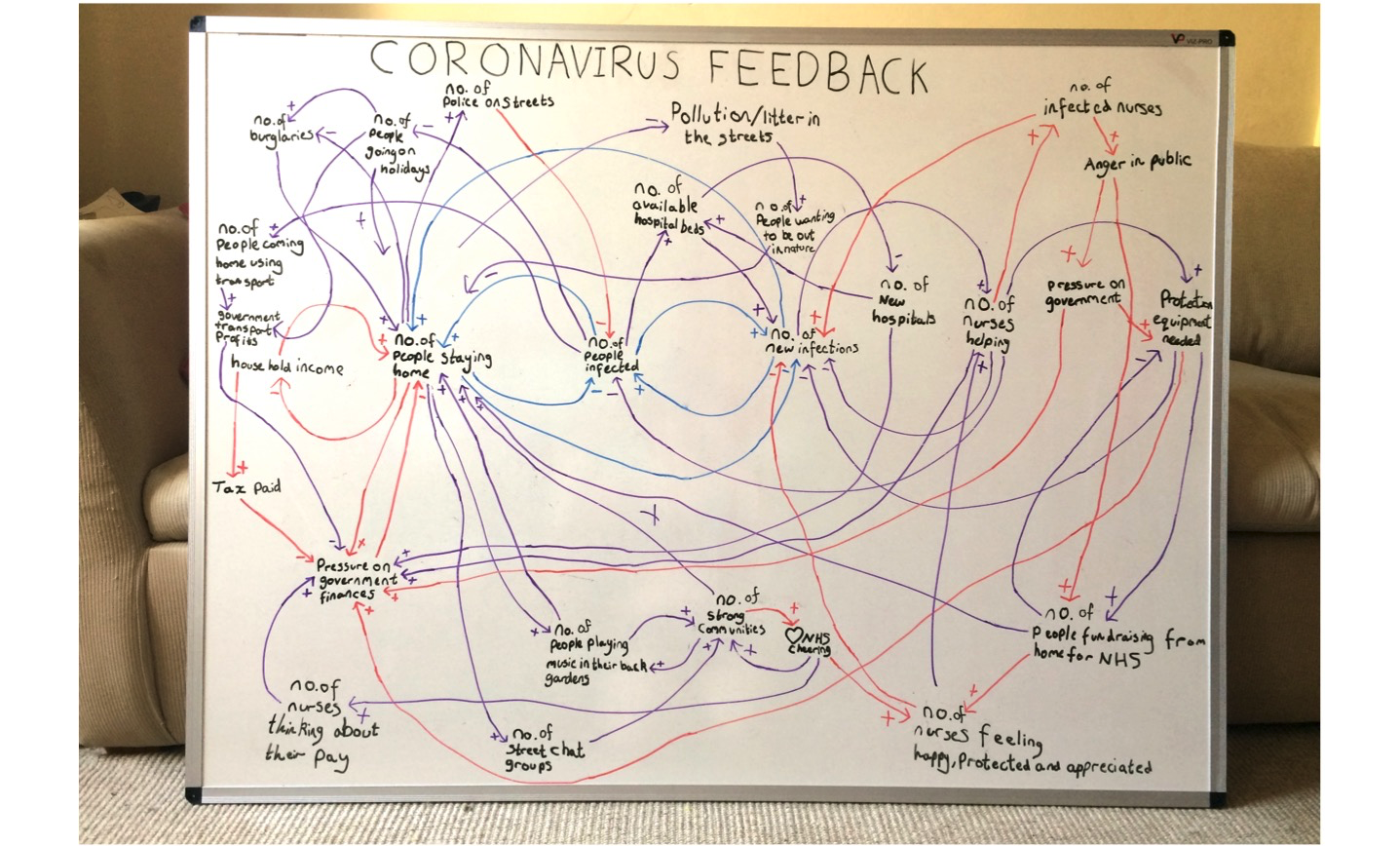
The high-level picture

When you make the model higher-level than “arbitrary code”, you get the side-benefit that you can now compile the model into multiple different types of code for different scientific tasks.

Part 2: Who is AlgebraicJulia?

History

• Evan Patterson started Catlab in 2017 to be a computer algebra system for applied category theory
• James Fairbanks started SemanticModels.jl in 2018 to achieve this “high-level modeling” dream
• In 2019, they started collaborating and created the AlgebraicJulia organization to maintain a variety of packages (often prefixed by “Algebraic”) around scientific modeling with applied category theory
• I joined in 2020 (the inflection point)
• Companies like Merck now hire based on “experience with AlgebraicJulia”

Ham up the connection between me joining and our present success.

Collaborators

(made with Semagrams)

collaborators = FileAttachment("collaborators.sema").text()

import { GraphApp } from "/main.js"

div = document.getElementById("collaborator-semagram")

GraphApp.main(div, collaborators)

• The main institutional support for Catlab comes from Topos and University of Florida
• Flex that the diagram is editable by moving Kris to Topos

Part 3: What is AlgebraicJulia

The landscape of AlgebraicJulia

Package	Description
Catlab.jl	Data structures, algorithms, visualization, computer algebra
AlgebraicDynamics.jl	Open dynamical systems
AlgebraicPetri.jl	Petri nets operations, including rate equation simulation
AlgebraicRewriting.jl	Rewriting systems for combinatorial data structures
AlgebraicRelations.jl	Database integration
CombinatorialSpaces.jl	Meshes for PDEs
Decapodes.jl	Discrete Exterior Calculus
StockFlow.jl	Stockflow diagrams and simulations
Semagrams.jl	User interfaces built around graphical syntax (Scala.js+Julia)

Don’t go through this in depth, just say “we have a lot of packages, we’re going to dive into the specifics of two of them”.

“The core package is Catlab, and then we have a bunch of ‘satelite’ packages”

Open dynamical systems overview

Libkind, Baas, Patterson, et al. (2022)

A hierarchical model of an ecosystem

Solving the dynamics for that ecosystem

Figure 2: Ecosystem modeling in AlgebraicJulia.

• Ecosystems are often composed out of many interacting parts
• Category theory lets us capture this compositional structure
• AlgebraicJulia allows us to compute the composition, and then simulate the ecosystem together

The math of open dynamical systems

(Vagner, Spivak, and Lerman (2015)) An open dynamical system consists of a state manifold \(X\), an input manifold \(X_{in}\), an output manifold \(X_{out}\), a readout function \(X \to X_{out}\) and an evolution function \(X \times X_{in} \to T X\).

Open dynamical systems form an operad algebra of the operad of undirected wiring diagrams.

[citation needed]

Multiphysics

Patterson et al. (2022)

In fundamental physics, we generally assume there is a single foundation for our reality, and thus only “one equation” to solve. However, in practice we model large-scale phenomena with a large variety of equations because solving the fundamental equations is too hard, so we pick approximations suitable for given domains. Classical mechanics, thermodynamics, fluid mechanics, and electromagnetics are all such approximations. However, the real world does not always come in discrete problems which can be partitioned into exactly one well-studied category of physics. Often, models contain multiple different types of physics, which need to talk to each other in order to solve the overall problem. We call this “multiphysics”, and it is as hard as it sounds, especially when you want to actually compute numerical solutions to multiphysics problems on the computer. Unlike ODE solvers, there are so many degrees of freedom in the choice of numerical approximation for PDE solvers that general-purpose PDE solvers are quite difficult to write, and most high-performance PDE solvers use specialized computing for a specific physics problem.

The AlgebraicJulia approach to multiphysics is to use a theory called the Discrete Exterior Calculus, which allows one to state physics problems in a way that makes clear some distinctions blurred by classical PDEs that are essential for efficient and accurate numerical computing. This already puts us at an advantage against traditional PDE solvers, but we also (need to ask more about story for interfacing between different physics).

Conjugate heat transfer

Heat transfer between a solid and a fluid

• The circles are heated solids
• Heat transfers from the solid to the liquid

Part 4: How is AlgebraicJulia?

What does it mean to “do category theory” on a computer?

• We have a different vision from the functional programmers
• Instead of just working with the category of types and functions, we manipulate values and expressions that represent objects and morphisms in categories. The manipulation itself may not be pure/mathematical, and might use mutation/imperative programming, but that’s fine; it’s happening at a different level from the actual category theory.
• This is a style of computational category theory that is somewhat unique to AlgebraicJulia, and very distinct from the style of computational category theory that the type theory community uses.

The problem: pushouts in FinSet

Figure 3: A pushout in \(\mathsf{FinSet}\)

In the category \(\mathsf{FinSet}\), the pushout of the above diagram is given by:

\[ X \sqcup_Z Y = (X + Y)/\sim \]

where \(\sim\) is the equivalence relation generated by \(f(z) \sim g(z)\) for all \(z \in Z\).

We want to actually compute pushouts!

Take time so that people can match up the diagram to the lemma.

FinSet in Julia

We first need to represent finite sets on the computer

# The finite set {1,...,n}
struct FinSet
  n::Int
end

# The function i ↦ values[i]
struct FinFunction
  dom::FinSet
  codom::FinSet
  values::Vector{Int}
end

A, B = FinSet(3), FinSet(2)
f = FinFunction(A, B, [1,2,2])

A data structure for partitions

Julia has a data structure for representing a partition of \(\{1,\ldots,n\}\).

using DataStructures

const Partition = IntDisjointSets

# A partition of {1,...,10}
a = Partition(10)
# Mutate a to make 3 and 5 be in the same equivalence class
union!(a, 3, 5)
union!(a, 5, 7)
# Compute representative of equivalence class
find_root!(a, 3) == find_root!(a, 7)

true

Pushouts in Julia

function pushout(X::FinSet, Y::FinSet, Z::FinSet,
                 f::FinFunction, g::FinFunction)
  # Start with the singleton partition of {1,...,|X|+|Y|}
  a = Partition(X.n + Y.n)

  # Construct the partition we want: f(z) ~ g(z) for all z ∈ Z
  for z in 1:Z.n
    union!(a, f.values[z], g.values[z])
  end

  # Return a FinSet of size the number of unique roots
  FinSet(length(unique!([find_root!(i) for i in 1:length(a)])))
end

This runs in time \(\mathcal{O}(m \log m)\), where m = X.n + Y.n.

Exercise: extend this code to also compute the legs of the cocone for pushout!

Part 5: Again, why is AlgebraicJulia?

• We talked about providing a high-level interface for scientists before
• Now we are going to talk about some other advantages that applied category theory has for scientific software development

Technical wins: data structures for free from C-sets

Patterson, Lynch, and Fairbanks (2022)

Figure 4: One data structure implementation, many data structures. Graphs, simplicial sets, petri nets, and undirected wiring diagrams.

Having high-level formal languages which are closer to the ways that scientists informally use category theory is great, but it’s not the only use of category theory in scientific computing. From a purely engineering standpoint, programming with category theory in mind has a great number of advantages because the abstractions from category theory can be used to avoid duplication of code. For instance, we have a generic data structures library based on functors from finitely presented category to Set (acsets), and we have algorithms for limits and colimits written for all of these. This gives us “for free”:

• Graphs
• Directed wiring diagrams
• Undirected wiring diagrams
• Petri nets

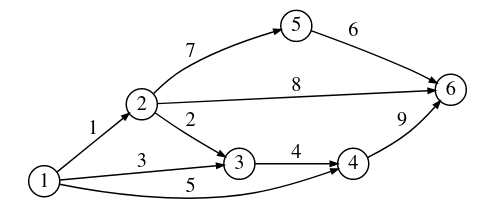
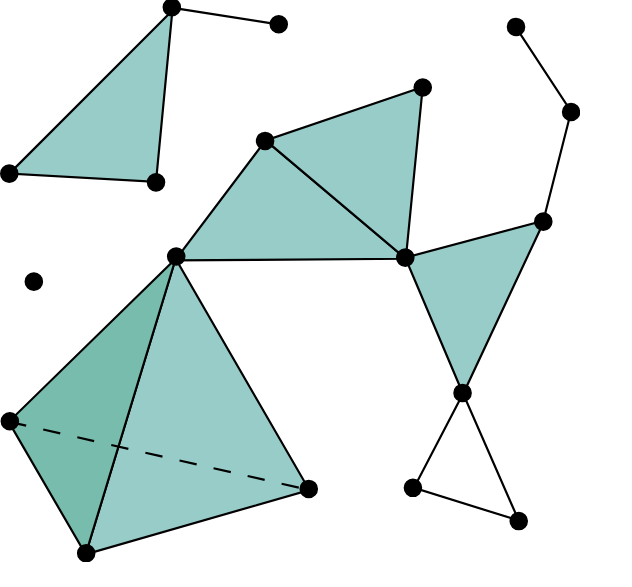
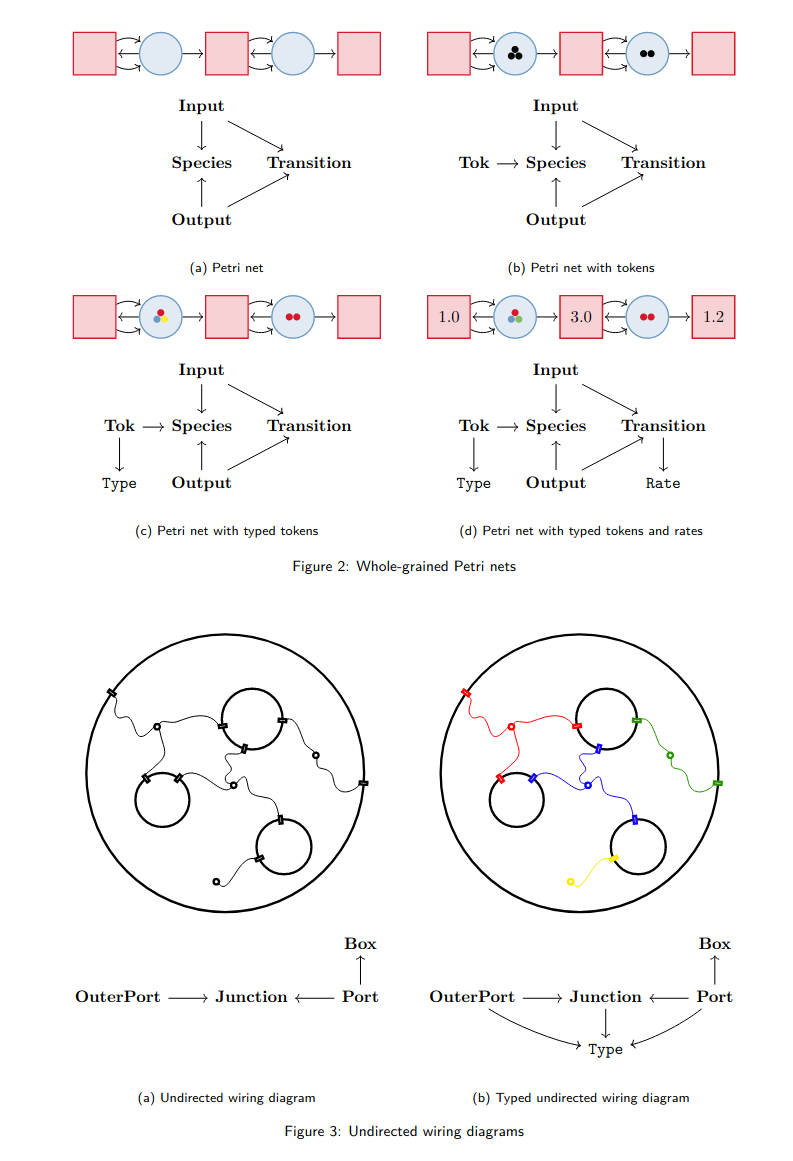
Technical wins: algorithms for free from limits/colimits

• Compute connected components for a graph by coequalizing src and tgt

• Split up a population in a Petri net by (age group/vaccination status/region/etc.) using limits (Libkind, Baas, Halter, et al. (2022))

We have generic algorithms to compute limits and colimits of any acset, and limits/colimits solve a variety of concrete problems

The fact that our software is so generic means that we have to write less code overall, which means that we can invest more time in quality, performance, and correctness, and improvements to our base algorithms and data structures reap benefits in all of our application areas.

Technical wins: algorithms for free from limits/colimits

• Compose structured cospans (c.f. Baez and Courser (2020)) of Petri nets

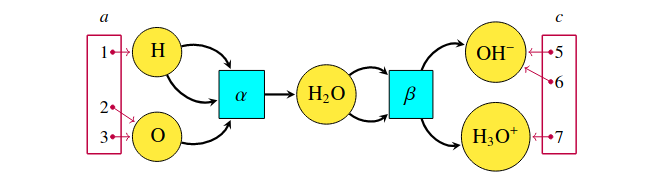
• Compose operations in the operad of (directed/undirected) wiring diagrams

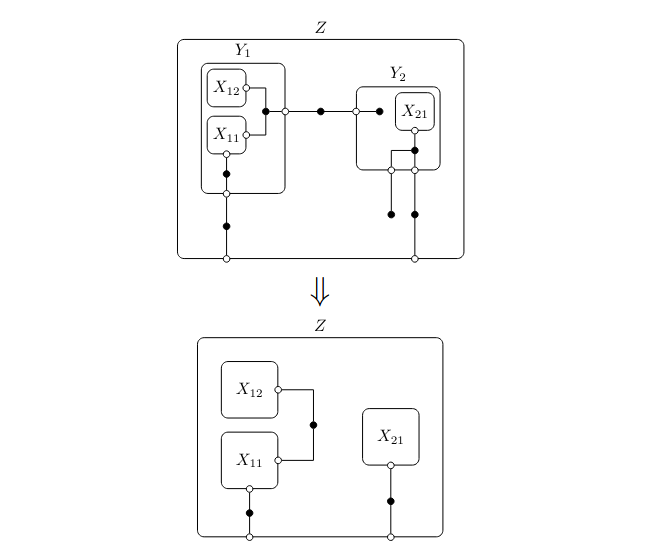
Compositional modeling

Halter et al. (2020)

• One of the rallying cries of applied category theory is “compositionality”.
• The AlgebraicJulia project takes compositionality and makes it work in software tools for scientists

The Future of AlgebraicJulia

1. Deliver high-quality results for individual domain-specific grants.
2. Along the way, carefully develop and refine general-purpose open-source tools for scientists solving the world’s problems.

Domain	Funders and Collaborators
Epidemiology	ASKEM DARPA Project, University of Saskatchewan, DARPA YFA award (PI: Fairbanks)
Multiphysics	ASKEM DARPA Project
Task modeling and planning	PTG DARPA Project
Industrial process and data management	CMU, NIST, Chevron
Compositional statistical modeling	AFOSR YIP award (PI: Patterson)
Education and outreach	Mozilla

What can you do…

• …if you will be on the job market soon:

  Topos Institute and James’s lab at University of Florida are growing and will be looking for researchers over the next couple years. There may not be positions lining up precisely with the timing of when you are looking, but keep in touch with us if this is something you are interested in.

• …if you want to use AlgebraicJulia?

  Read papers and blog posts on algebraicjulia.org, and then ask us questions in the Julia Zulip: julialang.zulipchat.com.

• …if you want to make your math be useful for scientists?

  There’s no magic bullet, but the two things that will help are

  1. Keeping the end goal in mind: category theory as UI for high-level formal scientific modeling
  2. Talking to us (the AlgebraicJulia crew) about your research!

References

Baez, John C., and Kenny Courser. 2020. “Structured Cospans.” arXiv. https://doi.org/10.48550/arXiv.1911.04630.

Brown, Kristopher, Tyler Hanks, and James Fairbanks. 2022. “Compositional Exploration of Combinatorial Scientific Models.” arXiv. https://doi.org/10.48550/arXiv.2206.08755.

Halter, Micah, Evan Patterson, Andrew Baas, and James Fairbanks. 2020. “Compositional Scientific Computing with Catlab and SemanticModels.” arXiv. https://doi.org/10.48550/arXiv.2005.04831.

Libkind, Sophie, Andrew Baas, Micah Halter, Evan Patterson, and James Fairbanks. 2022. “An Algebraic Framework for Structured Epidemic Modeling.” Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 380 (2233): 20210309. https://doi.org/10.1098/rsta.2021.0309.

Libkind, Sophie, Andrew Baas, Evan Patterson, and James Fairbanks. 2022. “Operadic Modeling of Dynamical Systems: Mathematics and Computation.” Electronic Proceedings in Theoretical Computer Science 372 (November): 192–206. https://doi.org/10.4204/EPTCS.372.14.

Patterson, Evan, Andrew Baas, Timothy Hosgood, and James Fairbanks. 2022. “A Diagrammatic View of Differential Equations in Physics.” Mathematics in Engineering 5 (2): 1–59. https://doi.org/10.3934/mine.2023036.

Patterson, Evan, Owen Lynch, and James Fairbanks. 2022. “Categorical Data Structures for Technical Computing.” Compositionality 4 (December): 5. https://doi.org/10.32408/compositionality-4-5.

Vagner, Dmitry, David I. Spivak, and Eugene Lerman. 2015. “Algebras of Open Dynamical Systems on the Operad of Wiring Diagrams.” arXiv. https://doi.org/10.48550/arXiv.1408.1598.